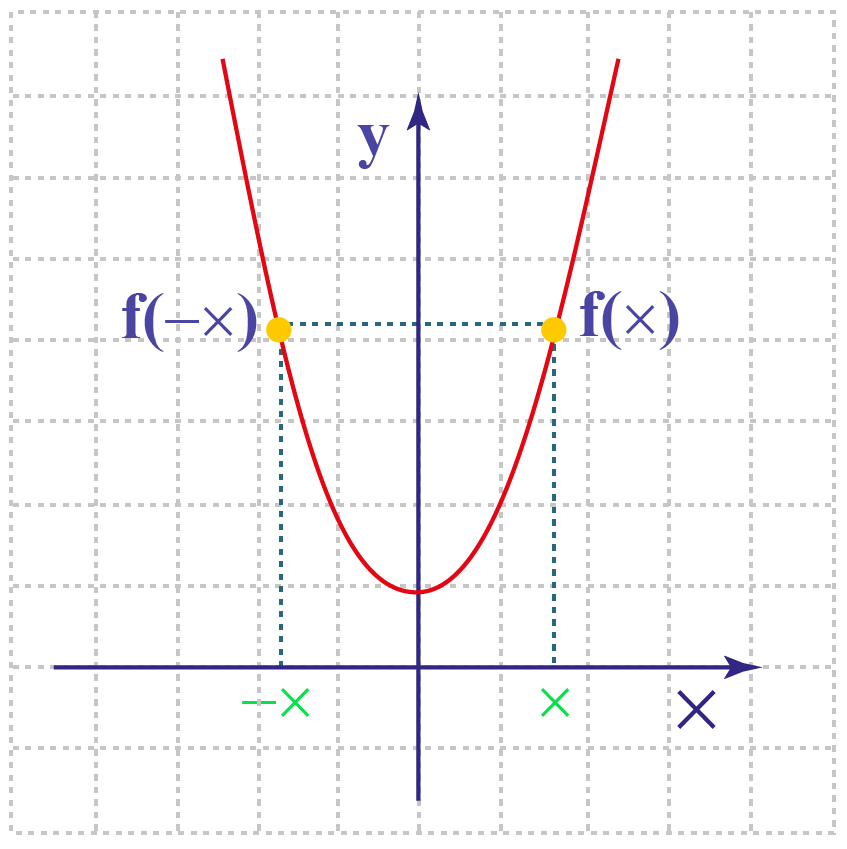
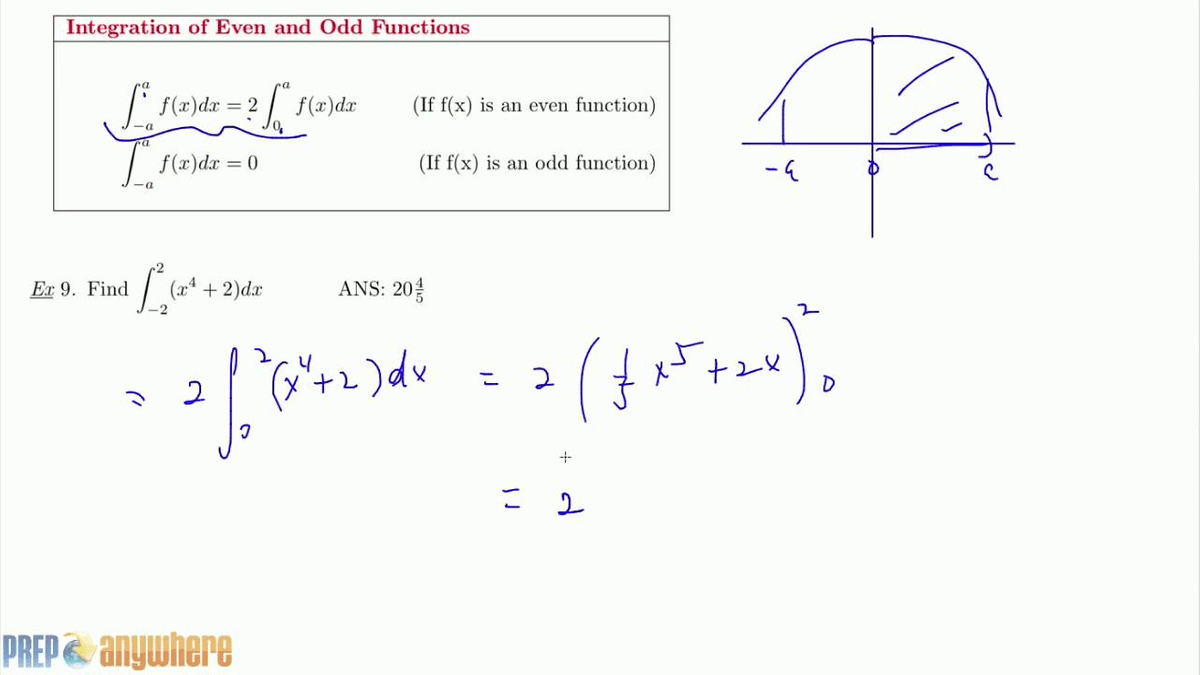Even Functionįor all values of x in the domain of f, a real-valued function f(x) is said to be an even function if the output value of f(-x) is the same as f(x).
Even and odd functions have the same symmetry. To test whether a function is even or odd, we substitute -x for x in the function f(x), checking the output value of f(-x) to ascertain the function type. Even and Odd FunctionsĪ real-valued function is either even or odd in most cases. A function can be even, odd, or both, or neither even nor odd.
The power function f(x) = x n is an even function if n is even, and an odd function if n is odd, hence even and odd functions are named accordingly. The symmetry relations of even and odd functions are used to classify them. Even and odd functions can be tested by substituting negative inputs (-x) for x in the function f(x) and examining the resulting output value. We can use algebra or graphics to determine whether a function is even or odd. There are various sorts of functions that we learn in mathematics.